THE CAVITATION THEORY OF MATTER

dcgeorge.com

The personal website of Douglas C. George.

The Cavitation Theory Of Matter

Abstract

A hole in the fabric of space itself—a cavitation bubble in the spacetime manifold—would be gravitationally indistinguishable from an ordinary massive object and would point to a simple and intuitive description of both matter and the gravitational field. If space has intrinsic mass and a positive cosmological constant, a rapid enough expansion of the universe could produce these cavities in great numbers

Introduction

In this paper, a hypothetical, spheroidal cavity in the spacetime manifold is shown to be gravitationally equivalent to a normal massive object, a conclusion implying that all matter may ultimately be, like black holes, constructed of nothing more than warped regions of space.

The nature of empty space has long been a controversial subject within the scientific community. Opinions about its nature have, over the years, covered a broad spectrum of conjecture ranging from it being absolutely nothing—an “empty box” so to speak—to it being some sort of fluid-like manifold that is flexible, stretchable and having a mass of its own independent of the material objects and radiation contained in it.

Whether or not empty space has a mass of its own has emerged, in recent years, as a subject of both laboratory experiment (the Casimir effect) and astronomical observations indicating that the expansion of the universe is accelerating. Because of these and other developments, space is now generally considered to have an intrinsic mass which is proportional to the cosmological constant Λ (lambda). This paper uses the term “lambda vacuum” for such a space and explores the possibility and ramifications of a particular type of discontinuity existing in it, namely: holes or bubbles analogous to the cavitation bubbles created by underwater propellers.

The concept of discontinuities in space is, in general, not a new or controversial idea. General relativity allows for many such oddities over a wide range of realistic models. It is widely accepted that space can have holes or edges where the mathematical values describing those regions can explode to infinity or come to an abrupt end.

If the lambda vacuum is considered to be an infinite, perfect-fluid manifold, a spherical cavity in it would be completely defined by the energy density gradient in the fluid surrounding the cavity. The gradient would be spherically symmetrical and would range from zero at the cavity boundary up to the average universal energy density at infinity. The cavity boundary would demarcate the edge of space itself.

The spherical symmetry of the gradient means that, by Birkhoff's Theorem, the exact exterior solution to the Einstein Field Equations for such a cavity must be the Schwarzschild metric, i.e., the metric of space surrounding a cavitation bubble in a lambda vacuum would be gravitationally indistinguishable from the metric of space surrounding any spherically symmetric massive object.

We will begin with a brief overview of the Schwarzschild solution to the Einstein Field Equations for a normal, spherical, uncharged, non-rotating, massive object. In particular we will focus on those problem areas of the metric—where the metric displays singularities and infinities—and then show that the metric of space describing a spherical cavity would be, except for the cavity itself, free of such complications.

The Ground Rules

“ ... In a word, matter may be just another form of space. ”
Dr. Sten Odenwald

General relativity treats space as a physical manifold that can expand, contract or be otherwise distorted by material objects embedded in it. Material objects are intimately related to the surrounding space and that relationship is made explicit by the Einstein Field Equations (EFE). A massive object is said to distort its surrounding space and the distorted space, in turn, determines how other objects will move through the area. In short, the distorted space is the gravitational field.

The physical properties of the vacuum have been, in recent years, a subject of intense and ongoing investigations. This paper will not speculate on the basic structure of space other than to accept that it has intrinsic mass and fluid-like properties. For simplicity, then, we will assume the vacuum to have a mass of its own and to be an infinite, idealized, compressible fluid with no viscosity and no heat conduction.

The warpage of a region of spacetime is related by the Einstein Field Equations to the flux of energy and momentum through the region. The field equations may be written as

  G_ab= kT_ab     [1]

where G_ab is the Einstein Tensor, T_ab is the stress-energy tensor and k is a constant. The Einstein tensor represents how space is distorted by the presence and flux of matter and radiation as accounted for in the stress-energy tensor.

The Schwarzschild vacuum solution to the field equations describes the geometry of space and time exterior to a spherical, non-rotating, uncharged massive object. It describes the warpage of the space as a function of the proper radial distance r from the center of the object. The geometry 1  is described by the following metric (in units where the speed of light is equal to one):

       [2]

The quantity ds is the invariant spacetime interval, t is the time coordinate, r is the radius of a sphere, Ω (Omega) is the standard interval of spherical solid angle and r_s is the Schwarzschild radius.

The Schwarzschild radius is the critical size for an object of a given mass at which gravity overwhelms all other known forces. It depends on the mass of the object according to the following equation:

     r_s = 2 GM /c ² ,       [3]

where G is Newton's gravitational constant, M is the object's mass and c is the speed of light. In the discussion of black holes that follows below, the term “Schwarzschild radius” is used interchangeably with the terms “critical radius” and “event horizon”.

The invariant interval ds represents the absolute measure of distance between two events in space and time and is the same for all observers regardless of their relative motion.

At a given instant of time, the proper radial distance, the actual distance between two points separated by an interval dr , as measured by a stationary observer positioned at radius r , is the square root of the radial component of the above metric and is equal to

     ( 1 − r_s / r ) ^{− 1/2} dr ,       [4]

which is greater than the same interval as it would be measured in flat, Euclidean geometry. It is this radial component of the metric that will be important in the arguments that follow because it is what determines the variations in the energy density surrounding a hypothetical cavity in space.

Black Holes

“ ... space and time may exhibit 'holes' or 'edges': spacetime singularities.”
Max Planck Institute for Gravitational Physics

Under certain conditions, the metric described in equation [2] in the preceding section implies the existence of black holes. If an object with mass M is compressed to its Schwarzschild radius, its gravity becomes so strong that no known force can halt its complete collapse. The mass will implode, crushing itself out of existence and leaving in its place a black hole.

As viewed by outside observers at rest with respect to the Schwarzschild metric, the space surrounding a black hole, like the space around any massive object, is well-behaved and the mathematics describing it contain no infinities or singularities. There are, however, two places where the metric appears ill-behaved: at the event horizon (where r = r_s ) and at the origin (where r = 0 ).

The Event Horizon

The event horizon r_s of an object depends, as expressed by equation [3] above, on its mass M . As r approaches r_s from the outside, a number of mathematical problems appear that demonstrate how the geometry is “ill-behaved”. Most relevant for the purposes of this paper, the geometry of space is stretched in the radial direction as described by equation [4] where, at the Schwarzschild radius, the stretching becomes infinite.

Although they can't be actually eliminated, the problems at the event horizon can be made “analytically removable” ²  by a change of coordinate system which allows a mathematical analysis to continue smoothly through the region.

Ill-behaved geometry at the event horizon can be considered to be artifacts of the particular frame of reference—the Schwarzschild coordinate system itself—and, as mentioned, can be made analytically removable. In a more appropriate reference frame—called the free-fall coordinate system—spacetime appears well-behaved all the way through the event horizon and down to (but not including) the central singularity. Using this special coordinate system, the Schwarzschild geometry appears to be that of ordinary, flat Euclidean space. Unfortunately, as we will see, this analytical taming of the metric comes with its own set of problems.

The free-fall coordinate system is the view of things as seen by an observer falling freely from infinity toward the black hole. Its distinctive feature (as well as the crux of its difficulties) is that space, itself, must be considered to be flowing radially inward at the Newtonian escape velocity:

     v = ( 2 GM / r ) ^1/2 .       [5]

This infall velocity of space starts out at zero at infinity, reaches the speed of light at the event horizon and continues to increase all the way to the central singularity where the velocity becomes infinite.

Because relativity theory limits the relative velocity of comoving objects to be less than the speed of light, if the infall velocity of an object reaches and then exceeds the speed of light, the argument asserts that it must be because space itself is flowing radially inward and carrying the coordinate system along with it.

So, in order to avoid the mathematical singularities and infinities at the event horizon, a coordinate system is used that drifts passively with a space that is assumed to be flowing toward the central singularity like water down a drain and which reaches infinite velocity just as it disappears from our universe.

While this coordinate system does circumvent the problems at the event horizon, it still leaves us with the problems at the central singularity and adds to those a new problem: if space has an intrinsic energy content, we are faced with the failure of the conservation of energy and momentum as space disappears at the central singularity.

In-between

The mathematics describing the region between the event horizon and the central singularity are, likewise, ill-behaved. There, space becomes “time-like”, time becomes “space-like”, the mathematics become imaginary (i.e., the geometry is represented by the square root of a negative number) and moving objects must be considered to travel backward in time.

As will be shown, a spherical cavitation bubble in space exhibits none of these problems but, first, let us examine more closely the problems at the central singularity.

The Central Singularity

Unlike at the event horizon, the central singularity is a true mathematical singularity. The problems there cannot be eliminated or made removable. It is the point where the mathematics of general relativity fail and, worse, until now there has been no way to get rid of it. At the central singularity, the Riemann tensor values representing the tidal stretching of space in the radial direction and the accompanying orthogonal tidal compressions become infinite.

According to the presently accepted view, the application of the metric to the space within the event horizon of a normal but highly compressed massive object leads to the mathematically inescapable conclusion that the object will implode and all of its matter will be crushed out of existence at the central singularity. The original imploding matter would be gone, completely. At the singularity, matter is stretched infinitely in the radial direction and squeezed infinitely in the orthogonal directions. Not only would the original matter be destroyed but any new matter falling past the event horizon in the future would be crushed out of existence at the central singularity.

The extraordinary thing here is that, even though all matter and radiation are completely destroyed, there would remain an enduring, pulsating shell of deformed space—the black hole—with none of the original matter left inside. All that remains is an empty shell of warped space. Even more remarkable is that, for outside observers, this empty shell of warped space still has all of the original mass!

To quote Kip Thorne ³ , the imploded matter is transformed into an object “made wholly and solely” from the warpage of space itself.

The original matter has apparently converted itself completely into deformations of space and it is those warpages, and nothing else, that subsequently possess all the mass.

So, here we have a massive object that appears to the outside world to be normal matter but has, in the usual sense, no material matter in it. That an empty shell of deformed space, devoid of matter, can be indistinguishable from an ordinary massive object, provides the first clue that matter itself might consist of nothing more than deformations of space. It is the position of this paper that this may actually be the case. We will argue that stable deformations of space may, in fact, not be limited to black holes but may be, in general, what both matter and its gravitational fields are made of.

A Hole in Space

The aim of the above discussion was to show briefly where and how the mathematics describing the space associated with a black hole displays well-known infinity and singularity problems. These problems have been known to physicists and mathematicians since shortly after the theory of general relativity was published in 1915 and are still seen as serious, if not fatal, flaws in the theory.

This paper introduces a theoretical structure, a pattern of warpage in space, that is not only gravitationally equivalent to normal matter (and compatible with the concept of black holes) but avoids all of the infinity and singularity problems associated with its metric and leads to a simple and intuitive description of both matter and its gravitational fields.

This structure—a cavity in space—may be more accurately described as a three-dimensional, spheroidal singularity in the spacetime manifold whose surface has the property of geodesic incompleteness and which demarcates the edge of space itself.

Since general relativity is a description of how space and matter are interrelated, it would be inappropriate to apply the mathematics of general relativity to the region inside such a cavity simply because space literally ends at the surface. Within the cavity, there would be—as Gertrude Stein said—no “there” there.

To see the details of such an object, how it would be constructed and how it might come to exist, we turn now to the topic of energy density gradients in a lambda vacuum. This portion of our discussion is aimed at those who have a fundamental knowledge of basic general relativity. It will be recognized that the arguments contain nothing new or unusual in the mathematics. It is simply basic general relativity as applied to the concept of a cavity in the fabric of the spacetime manifold.

Vacuum Density Gradients

“ ... you can't really separate the structure of space-time from the particles ...”
Michael Green (1988)

The energy density of the vacuum has, historically, referred to the distribution of normal matter and radiation dispersed in an otherwise mass-free space and is used in calculations predicting the evolution of the universe at large. For a lambda vacuum, however, where space itself has intrinsic mass, the energy density refers to the energy content of a region of space that is completely free of normal matter and radiation.

As mentioned previously, a lambda vacuum has an energy content of its own that is proportional to the cosmological constant Λ . It is equivalent to saying that the vacuum has a certain mass per unit volume (currently thought to be about 10 ^-29 g/cm ³ ). Collectively, this mass is said to comprise about seventy percent of all the mass in the universe, i.e., most of the mass of the universe is associated with the mass content of  “empty” space.

The cavitation bubbles proposed in this paper are defined as energy density gradients in such a space. So, the question here is whether or not it is possible for such energy density gradients to exist in a lambda vacuum.

Energy density gradients are, in fact, a normal part of general relativity. To see this we look at the relationship between the vacuum energy density of a region and the flux of momentum through the region as expressed by the stress-energy tensor of the field equations.

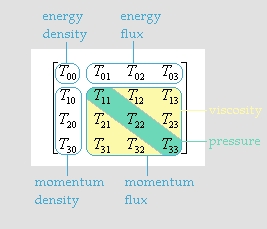
The illustration at the right shows the components of the stress-energy tensor T_ab in equation [1] above.

The energy density term in the upper left corner represents the energy density of a region and the three “pressure” terms arrayed along the diagonal highlighted in green represent the flux of momentum through the region in the x, y, and z directions. For an idealized fluid with no viscosity and no heat conduction, all of the other components of the tensor are zero.

This stress-energy tensor normally includes only the flux of energy and momentum associated with matter and radiation dispersed in an otherwise empty space. It does not include contributions from the space itself. If the space is considered to have a mass of its own, a new term, containing the cosmological constant, is added to the field equations.

The field equations with the cosmological constant added are:

     G_ab + Λg_ab = kT_ab ,       [6]

where the new term represents the contribution from empty space to the overall flux of momentum. This term can be moved to the right hand side of equation [6] and be considered as just another contribution to the stress-energy tensor shown in the illustration. For an empty universe (containing no material objects or radiation), the kT_ab term vanishes and only the stress-energy tensor representing the vacuum remains on the right hand side.

The net result is that the diagonal components in the illustration now represent the relationship between the energy density of the vacuum and the flux of distortions in the vacuum itself. In other words, since there are no normal massive objects or radiation in our simplified universe, the flux of energy can only be whatever energy density gradients happen to exist in, or are passing through, the space under consideration.

Formation of Cavities in Space and The Resulting Density Gradients

The spacetime manifold in our simplified model is assumed to have the properties of tension and compression so, if the metric stretching caused by the universe's expansion were to exceed the tensile strength of space, the vacuum would be brought to a foaming boil by the expansion. Cavitation bubbles would form in the fabric of space itself and the energy density would no longer be uniform. Around each cavity, an energy density gradient would form that starts out at zero at the cavity boundary and increases, in some fashion, back to the average density of the universe.

The Density Gradient Curve

The specific shape of the curve representing this energy density gradient would depend on the exact solution to the EFE for a cavitation bubble in a lambda vacuum. We know of no such solution that has been derived directly but, as mentioned above, because Birkhoff's theorem states that any exterior, spherically symmetric solution of the vacuum field equations must be given by the Schwarzschild metric, the exact solution in our case, likewise, has to be the Schwarzschild metric.

Taking, then, the Schwarzschild metric for the fluid surrounding such a cavity, what would be the mathematical form of the energy density gradient curve in the fluid?  

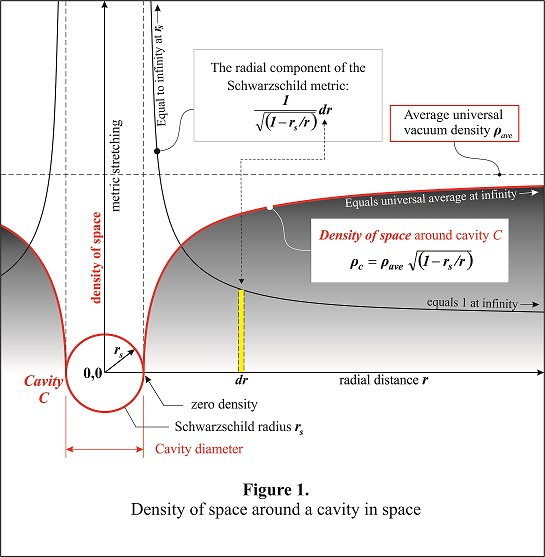
The radial component of the Schwarzschild vacuum metric (equation [4]) tells us that the metric of the space around each cavity would be stretched in the radial direction as a function of the distance from the center of the cavity.

Consider the example shown in Figure 1. which shows a cavity located at the origin of the coordinate system. The black curve is a plot of the radial component of the Schwarzschild metric and shows how measurements of distance are stretched as a function of the radial distance from the center of the cavity. The red curve shows the corresponding energy density of space around the cavity. As the metric stretching increases, the energy density of space goes down.

Therefore, in the space surrounding the cavity, we have an energy density gradient curve that is the inverse of the radial component:

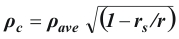      ,       [7]

The red curve in Figure 1. is a plot of Equation [7].

The Crux of the Argument

As can be seen in Figure 1, the slope of the density gradient curve increases as r approaches the origin from the outside and the amplitude of the curve goes to zero at the event horizon. The plot shows that the energy density of space thins out ever more rapidly as r approaches r_s .

Because the energy density of space goes to zero at the event horizon, the metric avoids all of the singularity and infinity problems at and within the event horizon. The upshot is that, for a cavitation bubble in a lambda vacuum, there are no singularity or infinity problems with the metric anywhere in space.

Motion of other masses

There are two ways to think about the effect on other objects exerted by the warped space surrounding these cavities.

In general relativity, for any specific region of space, the energy density and the flux of momentum are locally conserved. For a test particle moving through the area, its motion would be the only possible contribution to the flux of momentum. Consequently, the changing momentum of the test particle would be proportional to the negative of the radial component of the Schwarzschild metric. Its momentum, then, would just be the mirror image of the density gradient curve associated with the cavity M . In other words, the test particle's mass must increase and it must accelerate as it approaches the cavity.

The acceleration of the test particle would be proportional to the time derivative of the momentum divided by the particle's mass and would be calculated in the usual way from the metric and the field equations. Since the metric is the Schwarzschild metric, all calculations of motion would be the same as that for a normal material object moving through a gravitational field.

The other way to look at it is that since, by Birkhoff's Theorem, the space surrounding a cavity is distorted in the same way as it is by a normal massive object, the motion of a test particle must be identical to the motion of an object moving through a normal gravitational field.

To sum up the situation, if space undergoes an expansion rapid enough to produce cavitation bubbles and if the metric around those resulting cavities is the Schwarzschild metric the conservation law for energy and momentum tells us the resulting energy density gradients would have the same effect on other massive objects as gravitational fields produced by ordinary matter.

Gravitational fields may, therefore, be seen simply as energy density gradients in the vacuum: the simple thinning out (or thickening) of the density of space itself.

Black Holes vs. Ordinary Matter

We have, so far, drawn the similarities between a normal massive object, a black hole and a hypothetical cavitation bubble in a lambda vacuum. We have shown that they would be indistinguishable as viewed by outside observers and that the cavities would have problem-free metrics.

The basic cavities produced by an expanding universe would be tiny indeed. A cavity with the mass equivalence of an electron, for instance, would—according to equation [3]—have a Schwarzschild radius of ten to the minus fifty-seven meters which is twenty-two orders of magnitude smaller than the Planck distance. Quark-sized cavities would, according to their masses, have roughly similar dimensions.

The link between our theoretical cavitation bubbles and the plethora of known particles would depend on the details of the mechanical and electrical structure of the vacuum itself and is beyond the scope of the present paper. It is hoped that the reader will forgive us in what follows as we engage in some wild and shameless speculation about how these cavities in space would behave and interact.

We proposed, tentatively, that all matter may be constructed in the same way as black holes: as warpages of space and nothing more; the basic argument being that matter and black holes are both manifestations of cavities in space. Black holes would be large holes in space and the basic constituents of matter would be tiny ones. However, there is an obvious difference between a black hole and an ordinary massive object such as a planet or a star. Those objects, being full of ordinary particle matter, are definitely not empty shells of deformed space. This problem is resolved by recognizing that planets and stars would be comprised of sub-nuclear, foam-like agglomerations of un-coalesced cavities while black holes would result from the forced coalescence of those small cavities to form ever larger holes in space.

This way of looking at matter also offers a simple explanation for why the mass of a black hole is proportional to the square root of its surface area while that of a normal massive object like a planet is proportional to its volume. If a black hole is literally a hole in the fabric of space, it has no volume, as such, because it has no interior. Its entire description is its surface area and the way it warps its surrounding space. A normal object, being a foam-like collection of un-coalesced cavities, would have a mass that is proportional to the volume of the collection.

Since the building blocks of ordinary matter, in our scenario, would be constructed from sub-nuclear cavities in space, it is easy to think that, under sufficient gravitational pressure, they could be forced to coalesce into larger cavities. The coalescence of small cavities to form ever larger black holes is conceptually and theoretically simpler than crushing matter out of existence at the central singularity of a black hole or having space flow down a cosmic drain at infinite velocity. It would amount, simply, to gravity overcoming electrical and nuclear forces of repulsion between cavities.

Now consider the test particle mentioned above to, itself, be a small cavity. Its leading edge would always be in a steeper region of the density gradient produced by the large cavity than would its trailing edge. This means the leading edge would have a greater acceleration, causing the small cavity to be stretched radially and compressed orthogonally as described by the Schwarzschild metric in equation [2] (the term “spaghettification” applies here). If the leading edge were to reach the event horizon of the large cavity, the radial stretching of space there would be infinite.

The leading edge of the test cavity, then, would coalesce with the near edge of the large cavity at the common point where the density values of both go to zero, i.e., at the point where the two event horizons meet. A tunnel would open up between the two cavities and they would merge. After any transient oscillations die out, the large hole would be a bit larger than it was before (with its new mass still proportional to the square root of its surface area) and the small cavity would be gone. In our scenario, therefore, everything would appear the same as in the old paradigm but without the usual mathematical problems associated with the metric.

Summary

“ What else is there out of which to build a particle except spacetime itself?”
John Wheeler (1964)

If space is taken to be an infinite, ideal, fluid-like manifold with a positive energy density and if cavitation bubbles are somehow induced in this fluid, the resulting energy density gradients surrounding those cavities would be warpage complexes in space that are indistinguishable from ordinary material objects. If these sub-nuclear cavitation bubbles prove to be the basic building blocks of matter, a massive object and its associated gravitational field would be amalgamated into a single, complex pattern of warpage in space and nothing more. The idea of massive particles as entities distinct from the space in which they are imbedded would, therefore, be rendered superfluous.

This paper has argued that ordinary matter may be, like black holes, made wholly and solely from the warpage of space itself. The advantages of this paradigm are considerable. The entire structure of reality could be reduced to just one thing: the vacuum of space. It would be unnecessary to think that matter is crushed out of existence at the central singularity of a black hole; the conservation laws would be preserved; space wouldn't have to drain away into a cosmic sink-hole at infinite velocity; and there would be no mathematical problems associated with the metric anywhere in space.

1. For an excellent explanation of the geometry of space around massive objects, go to: http://casa.colorado.edu/~ajsh/schwp.html#radius . The “Ground Rules” section of this paper is based almost entirely on Mr. Hamilton's web site.
(back)

2. Being “analytically removable” is not the same as being completely eliminated. The singularity is removable, in the sense that all the invariant measures of the field smoothly approach fixed finite values as r approaches r_s . For the mathematically inclined, a detailed discussion of the issues surrounding the event horizon is given at: http://www.mathpages.com/rr/s8-07/8-07.htm
(back)

3. Kip Thorne, “Black Holes & time Warps: Einstein's Outrageous Legacy”, W. W. Norton & Company, 1994.
(back)